前言

感谢LeetCode让我又接触到了一个知识:sleeping:

极角排序

高中学习的极角，指的是极坐标系中的一个点相对极点有唯一的极坐标(\rho, \theta)，其中\rho表示选定点到极点的距离，\theta表示选定点和极轴逆时针的夹角，且0 \leq \theta \leq 2\pi。

极角排序方法一

直接通过反三角计算极角，我们知道极坐标和直角坐标转换公式中有\tan \theta=\frac{y}{x} ，所以可以用 arctan(\frac{y}{x})来计算。然而，arctan(\frac{y}{x})的值域只有\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)，并且\frac{y}{x}=\infty时无定义，所以需要复杂的分类讨论。不过在Golang以及Python中均有math.Atan2(y, x float64)以及math.atan2(y, x)可以直接计算点(x, y)的极角，且值域为(-\pi, \pi]，但是计算出来之后对应于笛卡尔坐标当中，第一第二坐标系为正，第三第四为负，从小到大关系为：第三象限→第四象限→第一象限→第二象限。

如果要按照极轴逆时针旋转扫过点的顺序来对点进行排序，那么可以将一二象限和三四象限的结果分别进行有小到大排列，最后进行拼接，就得到了最后的结果。

func angleSort(points [][]int, location []int) [][]int{
    points_1_2 := [][]int{}
    points_3_4 := [][]int{}
    for _,point:=range points{
        if point[1]-location[1]==0{
            points_1_2=append(points_1_2, point)
        }else {
            points_3_4=append(points_3_4, point)
        }
    }
    sort.Slice(points_1_2, func(i, j int) bool {
        return math.Atan2(float64(points_1_2[i][1]-location[1]), float64(points_1_2[i][0]-location[0]))<
            math.Atan2(float64(points_1_2[j][1]-location[1]), float64(points_1_2[j][0]-location[0]))
    })
    sort.Slice(points_3_4, func(i, j int) bool {
        return math.Atan2(float64(points_3_4[i][1]-location[1]), float64(points_3_4[i][0]-location[0]))<
            math.Atan2(float64(points_3_4[j][1]-location[1]), float64(points_3_4[j][0]-location[0]))
    })
    for _,p:=range points_3_4{
        points_1_2=append(points_1_2, p)
    }
    return points_1_2
}

极角排序方法二

除了直接使用math.Atan2直接计算极角之外，还可以使用向量积(叉积)的方式进行求解，如果有两个向量\vec{a}和\vec{b}，他们的叉积计算定义为|\vec{a} \times \vec{b}|=|\vec{a}| \bullet|\vec{b}| \bullet \sin \theta，其中\theta定义为a向量与b向量的向量积的方向与这两个向量所在平面垂直，且遵守右手定则。对于二维平面而言，如果\vec{a}和\vec{b}记为 [a.x, a.y]，[b.x, b.y]，那么计算公式可以记为(a . x * b . y-a . y * b . x)，因此比较这个值的大小就可以得出这两个端点被扫描的先后关系。但是仅靠叉乘是不能对一系列的点进行排序的，因为它不符合偏序关系的条件。如果通过不断在坐标轴上旋转，一个向量的极角最终会小于自己，但是位于同一象限的点是可以进行比较的，因此我们可以通过先比较象限的关系，在对比叉积的结果。

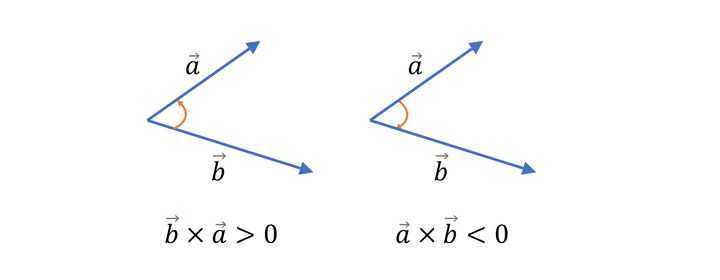
func angleSort2(points [][]int, location []int) [][]int{
    Q:= func(x,y int) int {
        if x>0 && y>0{return 1}
        if x<0 && y>0{return 2}
        if x<0 && y<0{return 3}
        if x>0 && y<0{return 4}
        return 0
    }
    sort.Slice(points, func(i, j int) bool {
        qi,qj:=Q(points[i][0]-location[0], points[i][1]-location[1]),Q(points[j][0]-location[0], points[j][1]-location[1])
        if qi!=qj{
            return qi<qj
        }else{
            return (points[i][0]-location[0])*(points[j][1]-location[1])-
                (points[i][1]-location[1])*(points[j][0]-location[0])>0
        }
    })
    return points
}

总结对比

两种方法都可以就对极角(或者相对关系的极角)进行排序，前者是绝对值，可以直接计算；后者是叉积的相对值，需要先进行象限判断再进行运算，多了一步。但是前者是float64结果，相对而言，如果需要精确的判断，那么前者可能会出现及其微小的误差，而后者属于整数运算，直接对比不会有误差。