Definition of diameter

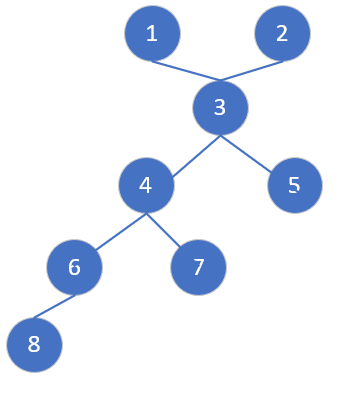
In a given tree, the diameter is defined as the longest path between any two nodes. For instance, the diameter of the tree shown below is 4, which is formed by the paths between nodes (1, 8), (2, 8), and (5, 8).

How can we obtain diameter of a tree?

Before calculating the diameter, we need to find the longest path in the given tree. It's worth noting that there may be multiple such paths, and any of them can be used.

Every longest path has two endpoints, such as nodes 2 and 8. Assume we start from node 3 and use either the DFS (Depth-First Search) or BFS (Breadth-First Search) algorithm to find the farthest node from node 3; we will eventually reach node 8.

Similarly, if we start from node 6, the farthest node will be either node 1 or node 2. Therefore, we can conclude that the farthest node retrieved from any starting node must be part of the diameter path.

In the next step, we should perform DFS/BFS from the identified farthest node (node 1, 2, or 8) to find the farthest node from it once again. This will give us the other endpoint of the diameter path.

Proof of Conclusion

The key point of the proof is to ensure that the node obtained in the first DFS/BFS is an endpoint of the diameter path.

Proof by contradiction

Terminologies:
s_n means start node of first DFS/BFS.
s_e means retrieved node of first DFS/BFS.
P_{dia} means diameter path.
P_{se} means path from start s to end e.

Proof

We start first DFS/BFS from node y to z and P_{dia} = P_{st}. Assume that y is not included by P_{st}. Here are some basic situations:

• 1) y is in P_{st}. Hence, P_{yz} > P_{yt} or P_{yz} > P_{ys}, that means P_{st} != P_{dia}. It contradicts with our proposition.

• 2) y is not in P_{st}, but P_{st} has common paths P_{xx^c} with P_{st}. Hence, P_{xz} > P_{xs} or P_{xz} > P_{xt} that means P_{yz} > P_{st}. It contradicts with our proposition.

• 3) y is not in P_{st}, and P_{st} has no common paths P_{st}. We can also know it contradicts with our proposition.

Implementation by Golang

The following Golang code block shows double DFS/BFS find out tree's diameter.

package main

func graphBuilding(edges [][]int) map[int][]int {
    graph := map[int][]int{}
    for _, edge := range edges {
        graph[edge[0]] = append(graph[edge[0]], edge[1])
        graph[edge[1]] = append(graph[edge[1]], edge[0])
    }
    return graph
}

func diameterOfTreeDfs(edges [][]int) int {
    graph := graphBuilding(edges)
    visit := map[int]bool{}
    var dfs func(node, dep int)
    maxDep := 0
    largestDepthNode := 0
    dfs = func(node, dep int) {
        if visit[node] {
            return
        }
        visit[node] = true
        if dep > maxDep {
            maxDep = dep
            largestDepthNode = node
        }
        for _, chd := range graph[node] {
            dfs(chd, dep+1)
        }
    }
    // from 1 (can be chosen randomly) to the largest depth
    dfs(1, 0)
    maxDep = 0
    visit = map[int]bool{}
    dfs(largestDepthNode, 0)
    return maxDep
}

Diameter Calculation by Dynamic programming

Propositions:

• Tree's diameter equals maximum diameter calculated by every node in tree.
• Single node's diameter equals the farthest pat plus second-farthest path retrieved from itself.

Here is DP code solution:

package main

import "sort"

func diameterOfTreeDp(edges [][]int) int {
    if len(edges) == 0 {
        return 0
    }
    max := func(x, y int) int {
        if x > y {
            return x
        }
        return y
    }
    graph := graphBuilding(edges)
    // still choose 0 as start point
    var dfs func(node, depth int) int
    visit := map[int]bool{0: true}
    ans := 0
    // query maximum depth from node to leaf node
    dfs = func(node, depth int) int {
        visit[node] = true
        mdep := depth
        depthes := []int{}
        for _, chd := range graph[node] {
            if visit[chd] {
                continue
            }
            d := dfs(chd, depth+1)
            mdep = max(mdep, d)
            depthes = append(depthes, d-depth)
        }
        sort.Ints(depthes)
        m := len(depthes)
        if m >= 2 {
            ans = max(ans, depthes[m-1]+depthes[m-2])
        } else if m >= 1 {
            ans = max(ans, depthes[m-1])
        }
        return mdep
    }
    dfs(0, 0)
    return ans
}