Timer on ProcessFunction and KeyedProcessFunction Flink distinguishes between two key notions of time: processing time and event time. Processing time refers to the system time at which an event is processed, whereas event time is explicitly defined or configu…
Stream API (SourceFunction, AbstractSourceFunction and RichSourceFunction) in Flink In Flink's streaming API, there is a critical interface named Function, which extends Serializable: public interface Function extends Serializable { } Nearly all streaming APIs…
Manhattan Distance Definition: The Manhattan distance between two points (x_1, y_1) and (x_2, y_2) in a 2D plane is defined as dis = |x_1 - x_2| + |y_1 - y_2|, where | \cdot | denotes the absolute value. Problem Definition Given a set of points {p_1, p_2, \ldo…
Why Dynamic Segment Tree? As know for segment tree, the space complexity is is up to 4n, which n is upper bound of data range. However, :-(, n some times becomes very large, such as 10^9 or infinity. OOM problem would occur if we allocate 4n size array for que…
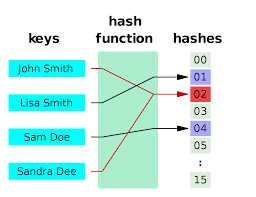
哈希(Hash) Hash又称为预映射,是通过散列算法将任意长度的输入变换成固定长度的输出,输出值称为散列值。这种转换是一种压缩映射,也就是散列值的空间通常远小于输入的空间,不同的输入可能得到相同的输出,所以不可能从散列值来确定唯一的输入值。 将输入映射为输出的过程可以称之为hash运算过程,常见的hash函数可以划分为:加法Hash;位运算Hash;乘法Hash;除法Hash;查表Hash;混合Hash;例如常见的MD5,MD4,SHA-1算法等,都是基于一系列的复杂的运算构成的。虽然运算过程复杂,但还是不可避免…
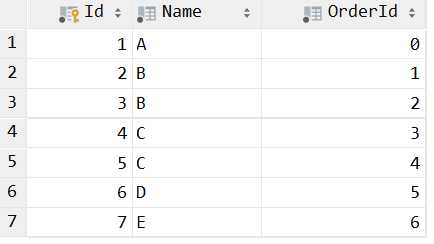
数据准备 创建两个表,一个存放用户信息,另一个存放用户订购的信息 CREATE TABLE IF NOT EXISTS `Customer`( `Id` INT UNSIGNED AUTO_INCREMENT, `Name` VARCHAR(100) NOT NULL, `OrderId` INT UNSIGNED NOT NULL, PRIMARY KEY ( `Id` ) )ENGINE=InnoDB DEFAULT CHARSET=utf8; CREATE TABLE IF NOT EXISTS `Order…
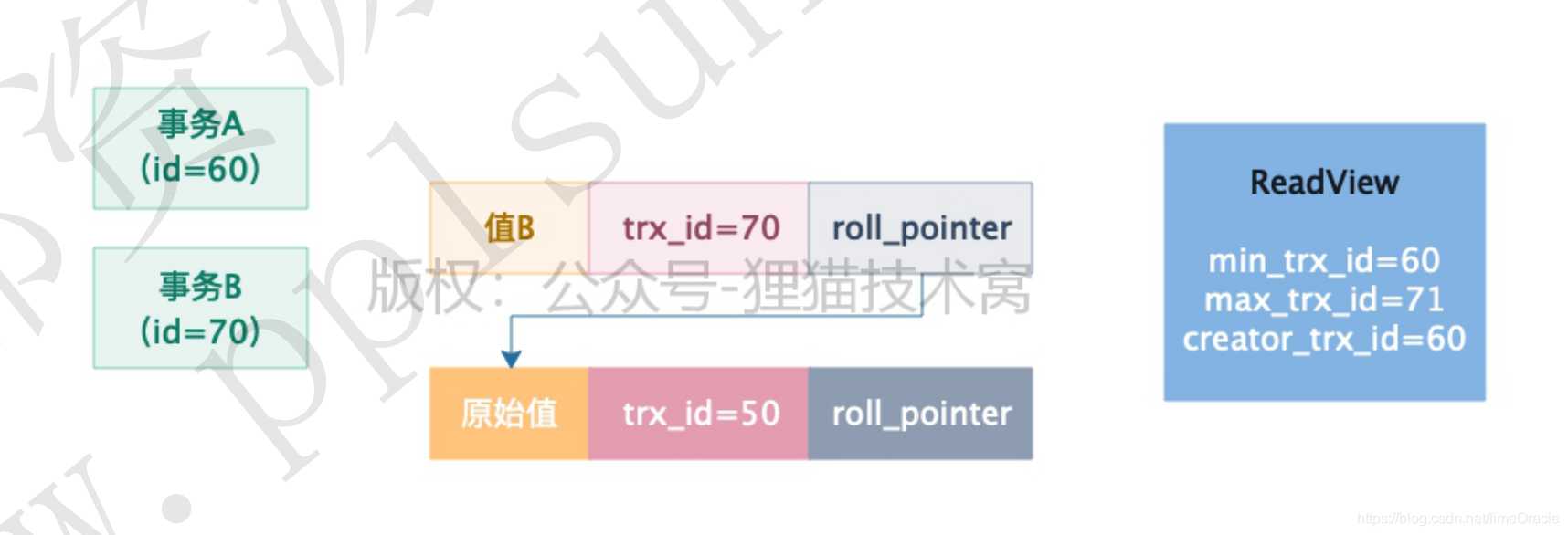
先说结论,MVCC不能完全解决幻读。只能解决快照读下的幻读,当前读的幻读依然需要借助next-key锁来解决幻读。 什么是幻读? 使用InnoDB作为引擎的MySQL有四种事务隔离级别,分别是: - Read Uncommitted:读未提交 - Read Committed:度提交 - Repeatable Read:可重复读 - Serialization:串行化 使用这些隔离级别可以解决数据读取时的脏读,不可重复读,幻读问题。其中脏读是指A事务读到了其他事物未提交的修改。不可重复读指的是同一个事务在相同查询条…