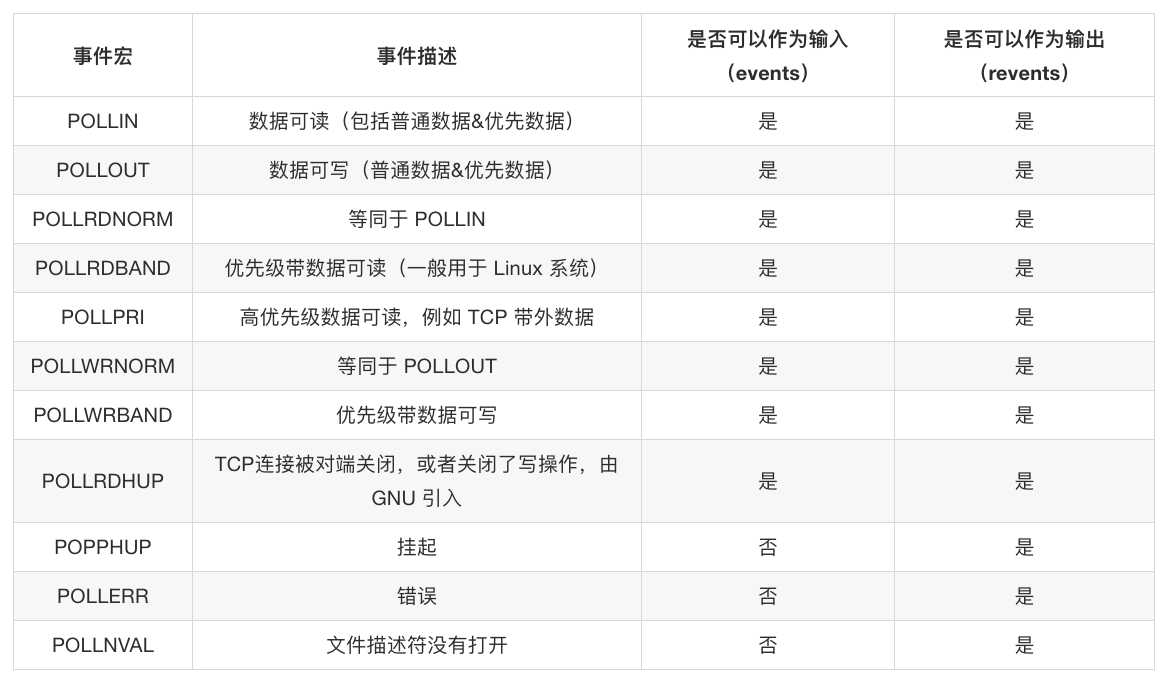
poll select, poll, epoll是IO多路复用当中的重要的三种实现方式，poll和epoll相对于select而言，只能在Linux下使用，但是select是跨平台的。同时poll相对于select而言，没有最大监听数量的限制。但是也是监管一系列的文件描述符，阻塞的去轮询看这些文件描述符是否可读/可写/异常，再去调用io函数读写。 但是select和poll都存在一个很大的“缺点”，当存在大量的连接且其中绝大部分的连接都是活跃的时候，那么poll/select的效率实际上是很低下的，这也是由于二者的…

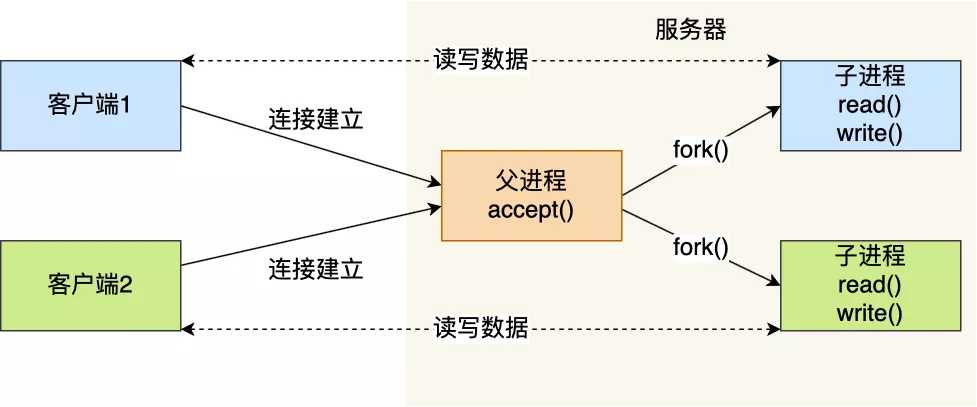
题外话：服务器单机理论最大能连接多少个客户端？ 答案是：对于IPV4而言，粗略估计有2^48个连接。计算机标识一个唯一的socket连接依赖的是唯一四元组-(源ip，源端口，本机ip，本机端口)，其中本机的ip和socket初始化的端口是不能变的，因此源ip和源端口都是可变的。那么本机的一个进程，理论上可以连接2^32*2^16=2^48个连接，32表示IPV4的地址数，2^16表示本机端口号的数目(65535)。 当然，理论值只是理论值。限制连接数的不只是ip和端口两个因素，还和内核的各种限制也有关系，每一个so…

摩尔投票是什么？ 摩尔投票用于寻找集合中出现多数的元素，并且出现多数可以定义为大于n//2或者n//3或者是其他自定义的频次(实际上，如果希望求出超过n//3频次的元素，那么是三个元素相互抵消)。摩尔投票的基本流程为： - 投票阶段：投票人之间进行抵消。 - 技术阶段：计算对抗结果中最后剩下的候选人票数是否有效。 投票环节 设置候选人candidate以及候选人的票数统计count的两个变量，每次遍历到一个元素的时候对当前候选人的票数进行抵消操作，当票数抵消到0时，选取新的候选人。伪代码如下： candidate,…

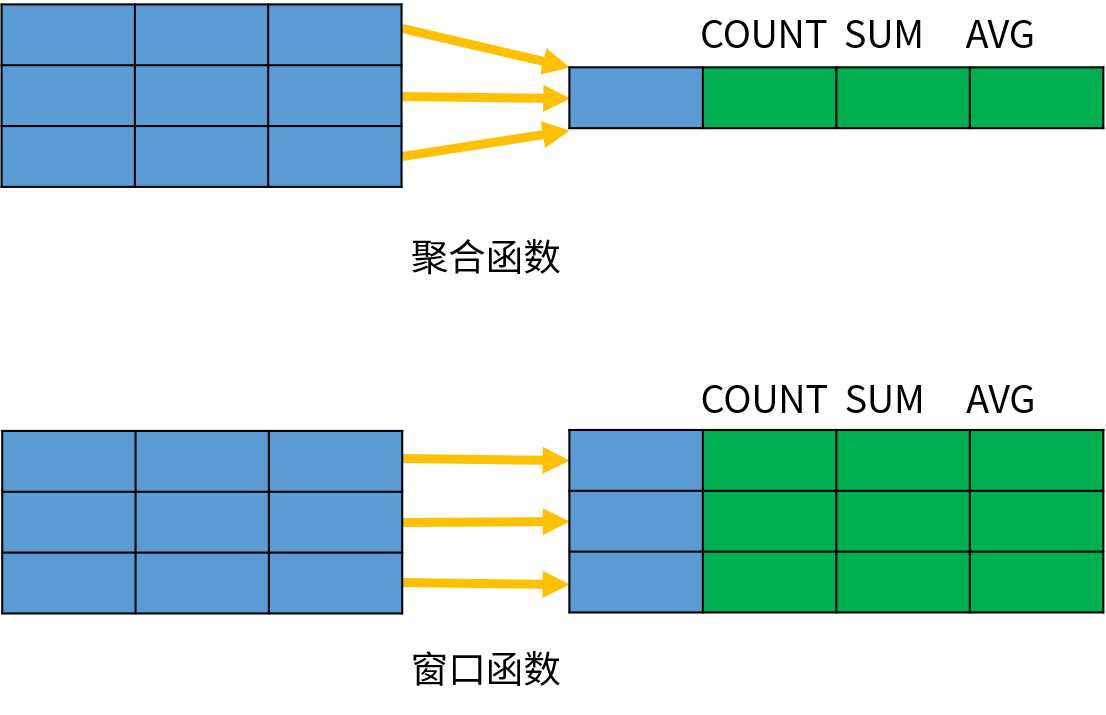
窗口函数概述 窗口函数（Window Function）针对查询中的每一行数据，基于和它相关的一组数据计算出一个结果。顾名思义，每一行都会对应一个计算结果，而不是将一组结果聚合计算成一条结果，原始数据有多少行，窗口函数计算之后还是有多少行。 创建数据 CREATE TABLE sales ( year INT, country VARCHAR(20), product VARCHAR(32), profit INT ); insert into sales(year, country, product, profi…

GROUP BY GROUP BY语句用于对指定的字段进行分类，之后用来与聚合函数(aggregate functions)例如统计(COUNT), 求和(SUM), 求平均(AVG), 求最小最大值(MIN/MAX)联合使用来得到一个或多个列的结果集。 基本的语法为： SELECT column1, column2, ... column_n, aggregate_function (expression) FROM tables WHERE condition1 [and/or condition2...] G…

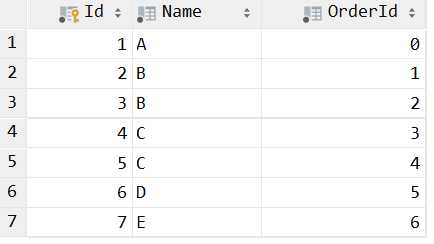
数据准备 创建两个表，一个存放用户信息，另一个存放用户订购的信息 CREATE TABLE IF NOT EXISTS `Customer`( `Id` INT UNSIGNED AUTO_INCREMENT, `Name` VARCHAR(100) NOT NULL, `OrderId` INT UNSIGNED NOT NULL, PRIMARY KEY ( `Id` ) )ENGINE=InnoDB DEFAULT CHARSET=utf8; CREATE TABLE IF NOT EXISTS `Order…

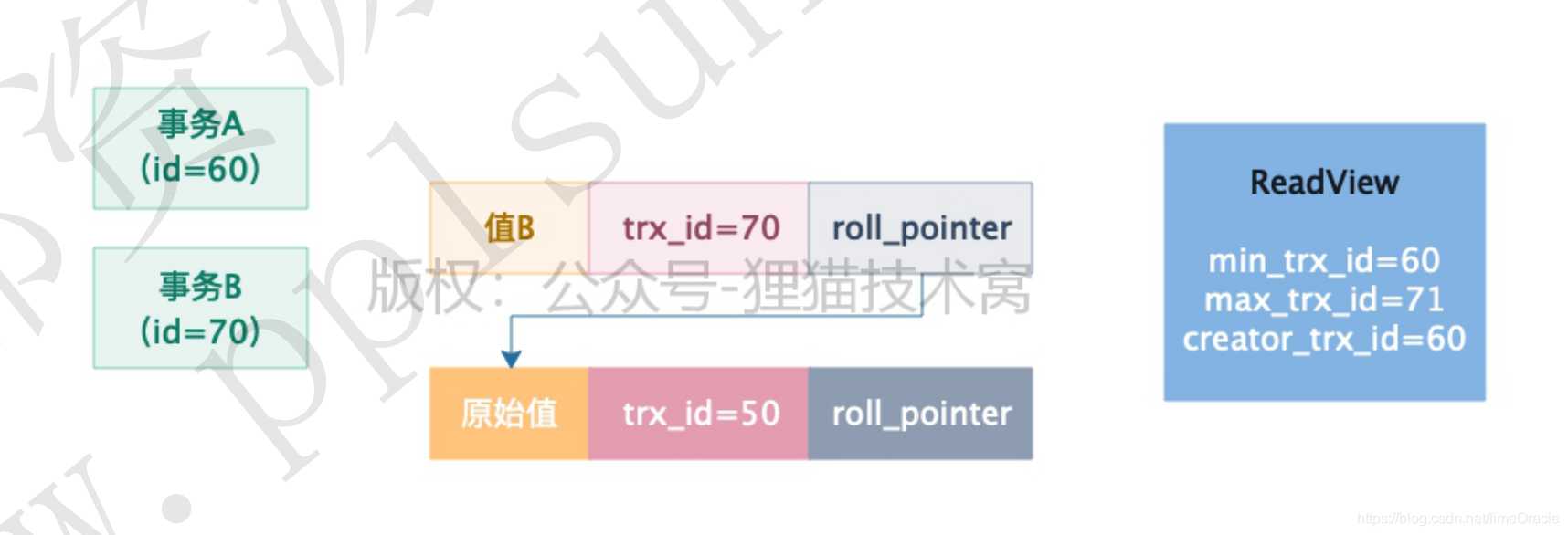
先说结论，MVCC不能完全解决幻读。只能解决快照读下的幻读，当前读的幻读依然需要借助next-key锁来解决幻读。 什么是幻读？ 使用InnoDB作为引擎的MySQL有四种事务隔离级别，分别是： - Read Uncommitted：读未提交 - Read Committed：度提交 - Repeatable Read：可重复读 - Serialization：串行化 使用这些隔离级别可以解决数据读取时的脏读，不可重复读，幻读问题。其中脏读是指A事务读到了其他事物未提交的修改。不可重复读指的是同一个事务在相同查询条…

类和对象 class关键词声明的类其实也是对象，比较特殊的是，它是type的实例对象。因此类也可以和对象一样作为参数进行传递等一系列操作。以下两种方法创造的类是一样的： # type(name, bases, attrs) ，name为类的名称，bases为需要继承的父类的集合，attrs为需要初始化的变量的值 Ex1=type('Example', (), {}) # type创造Ex1的类(不是实例对象) ex1=Ex1() # 实例化 class Example: # 手动创造 pass ex2=Exampl…

问题描述 完全背包问题和01背包问题不同的在于，每一个物体的数量可以是无限的，每一个物体的重量为C[i]，其产生的价值为 W[i]，一共N件物品。背包的容量为V。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量，且价值总和最大。 问题求解 和01背包问题的区别在于，01背包问题当中对应的是一个物品放入或者不放入两种状态 但是完全背包问题每种物体的状态是放置 0,1,2,3...个 按照01背包问题思路，当前能获得的最大值和只和上一个放入背包的物品数量有关，转移方程记录为： dp[i][v]=max(dp[…

01背包问题 问题抽象：有N个物体，每一个重量为c[i]，各自的价值为w[i]，背包最大容量为V,求背包能放下的物品总和的最大价值 DP思想解决问题 每一个物体都有被放入和不被放入的可能，当前被选择的物体是否被放入所产生的最大价值和后续的物体无关(无后效性)，只和前面已经放入的物体的总价值 有关(重叠子问题)，前面的最优，加上当前的物体一定最优(最优子结构) 转移方程 f[i][v]表示将第i种物体放入容量为v的背包能达到的最大价值 f[i][v]=max{f[i-1][v], f[i-1][v-c[i]]+w[i…